Blog reading: "Using Causal Inference to Improve the Uber User Experience"
https://eng.uber.com/causal-inference-at-uber/
In this post, two data scientists survey the internal landscape of causal inference techniques at Uber, providing some valuable insight into the state of causal data science in Silicon Valley. With some great flowcharts to boot!
The post is divided into two sections: one with techniques for use in the context of random experiments and another for observational contexts. There's a lot of ground covered in these flowcharts, so we'll have to go into more depth on some of these topics in later posts. (Uber has published more details in blogs and papers on a number of these topics.) Still, it's a great 5,000-foot view of how data scientists at tech companies are thinking about causal inference techniques today.
Random experiments
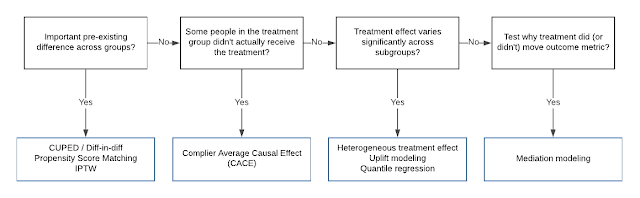
Why would we need causal inference techniques when we've already run a random experiment? Isn't causal inference supposed to be for situations where we don't have access to the gold standard of randomized control trials?
It turns out that randomization is not a catch-all solution. For one thing, with high-dimensional data and small datasets randomization might not actually produced balanced datasets like we hoped. We may need to use tools like inverse probability weighing, propensity score matching, or CUPED—"controlled-experiment using pre-experiment data"—to control for the covariate differences between groups that exist despite randomization.
There are other ways random experiments can go astray. The treatment variable may not be sufficiently indicative of actually being exposed to an intervention—e.g. if our treatment is sending an email we must encode the fact that some treated individuals may not ever read said email. We can address this by terming the users who read the email compliers—like patients who take their prescribed medicine—and computing the Complier Average Causal Effect (CACE).
A random experiment might not capture the fact that different strata of users experience vastly different treatment effects. We can use techniques such as uplift modeling and quantile regression to do heterogeneous treatment estimation—to take finer-grain measurements of treatment effects in different sub-populations.
Finally, even if our random experiment tells us something about some causal effect, we still needt to know why. For this, we can use techniques like mediation modeling for interpretability—introspection on why or why not some outcome metric changed.
Observational studies
As we've talked about before, causal inference from observational data is hard because of fundamental differences between the treated and control groups. One way to think about these differences is in terms of the causal graph. A covariate with a causal effect on both treatment and outcome will be a confounder in observational studies because a back-door path exists between treatment and outcome in the causal graph.
Doing causal inference in observational contexts involves accounting for these backdoor paths in one way or another. The flowchart gives a lowdown:
The simplest thing we could do is to only compare sets of users with similar covariate values—e.g., from the causal graph above, comparing treatment and control users who've made similar numbers of Uber Eats orders. But as our data grows in dimension we'll often run into problems of overlap: there may not be enough treatment and control data with similar covariates to compare. (A previous paper we've read on this blog addressed characterizing that overlap with simple, interpretable rules.) There are a few options for dealing with this. One is to simulate what we would have observed if the covariates were balanced using inverse probability weighting. A second is to compare treatment and control data that have a similar probability of treatment—the propensity score—even if the covariates themselves are not so similar.
If we have time-series data for both treatment and control groups before an after an intervention, we have other interesting options. One choice is to use Bayesian structural time-series models with synthetic controls. The idea here is fairly intuitive: given that we have treatment observations before the intervention and control observations both before and after the intervention, we train create a model that predicts what we would have observed had the intervention not taken place. The difference between this prediction and what we actually observed is the effect of the intervention. This is the approach taken by the popular R CausalImpact package, which we'll write about on this blog at some point in the future.
Further reading:
How Booking.com Increases the Power of Random Experiments with CUPED
Analyzing Experiment Outcomes with Quantile Regression
Heterogeneous Treatment Effects
Mediation modeling at Uber
Doubly Robust Estimation of Causal Effects
Inferring causal impact using Bayesian structural time-series models
In this post, two data scientists survey the internal landscape of causal inference techniques at Uber, providing some valuable insight into the state of causal data science in Silicon Valley. With some great flowcharts to boot!
The post is divided into two sections: one with techniques for use in the context of random experiments and another for observational contexts. There's a lot of ground covered in these flowcharts, so we'll have to go into more depth on some of these topics in later posts. (Uber has published more details in blogs and papers on a number of these topics.) Still, it's a great 5,000-foot view of how data scientists at tech companies are thinking about causal inference techniques today.
Random experiments
Why would we need causal inference techniques when we've already run a random experiment? Isn't causal inference supposed to be for situations where we don't have access to the gold standard of randomized control trials?
It turns out that randomization is not a catch-all solution. For one thing, with high-dimensional data and small datasets randomization might not actually produced balanced datasets like we hoped. We may need to use tools like inverse probability weighing, propensity score matching, or CUPED—"controlled-experiment using pre-experiment data"—to control for the covariate differences between groups that exist despite randomization.
There are other ways random experiments can go astray. The treatment variable may not be sufficiently indicative of actually being exposed to an intervention—e.g. if our treatment is sending an email we must encode the fact that some treated individuals may not ever read said email. We can address this by terming the users who read the email compliers—like patients who take their prescribed medicine—and computing the Complier Average Causal Effect (CACE).
A random experiment might not capture the fact that different strata of users experience vastly different treatment effects. We can use techniques such as uplift modeling and quantile regression to do heterogeneous treatment estimation—to take finer-grain measurements of treatment effects in different sub-populations.
Finally, even if our random experiment tells us something about some causal effect, we still needt to know why. For this, we can use techniques like mediation modeling for interpretability—introspection on why or why not some outcome metric changed.
As we've talked about before, causal inference from observational data is hard because of fundamental differences between the treated and control groups. One way to think about these differences is in terms of the causal graph. A covariate with a causal effect on both treatment and outcome will be a confounder in observational studies because a back-door path exists between treatment and outcome in the causal graph.
If we have time-series data for both treatment and control groups before an after an intervention, we have other interesting options. One choice is to use Bayesian structural time-series models with synthetic controls. The idea here is fairly intuitive: given that we have treatment observations before the intervention and control observations both before and after the intervention, we train create a model that predicts what we would have observed had the intervention not taken place. The difference between this prediction and what we actually observed is the effect of the intervention. This is the approach taken by the popular R CausalImpact package, which we'll write about on this blog at some point in the future.
Further reading:
How Booking.com Increases the Power of Random Experiments with CUPED
Analyzing Experiment Outcomes with Quantile Regression
Heterogeneous Treatment Effects
Mediation modeling at Uber
Doubly Robust Estimation of Causal Effects
Inferring causal impact using Bayesian structural time-series models
Comments
Post a Comment